LeetCode #1 – Two Sum

Let’s solve LeetCode 1 – Two Sum problem. It’s from the Arrays section on LeetCode, and we’ll tackle it using C# today.

There are often multiple ways to solve an algorithm. However, it’s crucial to consider the time and space complexity of your code. This is where Big O notation comes in. Understanding Big O notation is essential for developers to write efficient, scalable, and performant code.

Before we jump into the code, let’s understand the problem statement.

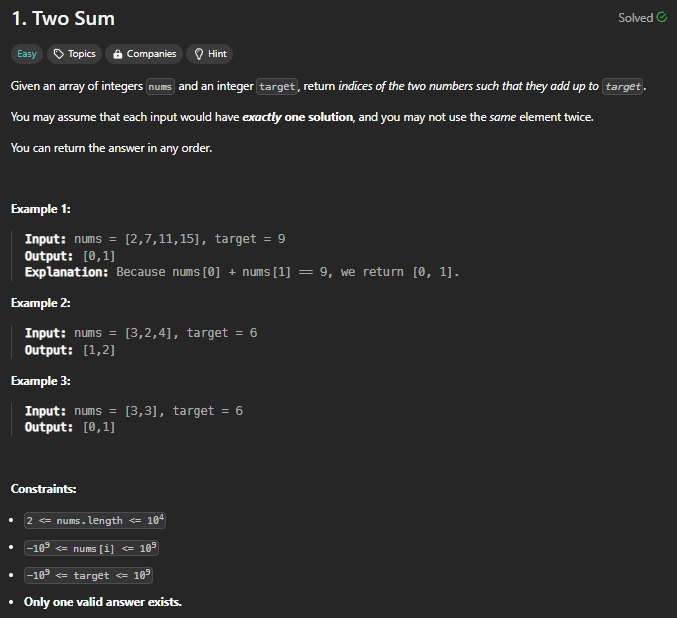
While the problem description itself is straightforward, finding the optimal solution can be tricky. You might initially consider using nested loops, which would result in a time complexity of O(n^2). This is not ideal for larger datasets due to scalability concerns. Fortunately, there are more efficient approaches available!

To solve this efficiently, let’s create a dictionary, and store each number of the array as its key, and the number’s index as its value. Our dictionary will look like this:

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        IDictionary<int, int> dict = new Dictionary<int, int>();
    }
}

We’ll create an array to store the solution: the indexes of the two numbers that sum to the target:

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        IDictionary<int, int> dict = new Dictionary<int, int>();
        var result = new int[2];
    }
}

This step might seem a bit tricky, so follow along closely.

We’ll iterate through the nums array. For each number, we’ll check if the dictionary contains a key equal to the difference between the target sum (target) and the current number of the loop. Remember, the dictionary keys are the numbers from the nums array.

Here’s why we check this: if the difference exists in the dictionary, it means the current number and the value stored for that key (which is the difference) add up to the target sum. These are the two numbers we’re looking for! And then we just have to assign these two numbers to the array we created earlier:

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        IDictionary<int, int> dict = new Dictionary<int, int>();
        var result = new int[2];

        for(int i = 0; i < nums.Length; i++){
            if(dict.ContainsKey(target - nums[i])){
                result[0] = dict[target - nums[i]];
                result[1] = i;
            }        
        }
    }
}

Since the dictionary is initially empty, we need to populate it with the numbers from the nums array and their corresponding indexes. This is crucial because the if statement we are using checks for the difference between the target sum and a number from the array. By storing the numbers and their indexes in the dictionary, we can efficiently look up the complement (the difference). So, below the if statement we need to add:

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        IDictionary<int, int> dict = new Dictionary<int, int>();
        var result = new int[2];

        for(int i = 0; i < nums.Length; i++){
            if(dict.ContainsKey(target - nums[i])){
                result[0] = dict[target - nums[i]];
                result[1] = i;
            }
            dict[nums[i]] = i;     
        }
    }
}

Now, we just need to return the result array after the loop!

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        IDictionary<int, int> dict = new Dictionary<int, int>();
        var result = new int[2];

        for(int i = 0; i < nums.Length; i++){
            if(dict.ContainsKey(target - nums[i])){
                result[0] = dict[target - nums[i]];
                result[1] = i;
            }
            dict[nums[i]] = i;            
        }
        return result;
    }
}

With this solution, our runtime beats 94.16% of users with C#!